路径规划之 LPA_Star (LPA*)

LPA*是 A*的增量版本. 相比于 A*算法, 首次规划时, 两者过程类似. 假如地图发生变化, A*算法需要重新规划路径. 而 LPA*算法可以通过在当前搜索期间内更新前一次搜索的 g 值（距起始距离）来适应地图变化而无需重新计算整个地图。

lpa_star.gif

算法描述

局部连续（Locally Consistent）：$g(s)=rhs(s)$。当所有节点均为局部连续状态时，g(s)的值等于 s 到起始点的最短距离（注意，反向不成立）。这个概念很重要，当上述条件满足时，我们可以找到任意一点 u 到起始点的最短路径，假设当前位置为 s,父辈节点 s’(向着起始点前进的下一个节点)通过最小化(g(s’)+c(s,s’))来获得，不断重复直到到达 sStart。然而，LPA*并不需要使所有节点均为局部连续状态，它通过启发式搜索将关注点放在搜索上，并且只更新那些与计算最短路径相关的节点的 g 值。

局部过连续（Locally Overconsistent）：$g(s)>rhs(s)$。当优先队列 U 中取出的节点为局部过连续状态时，意味着 g(s)可以通过父辈节点使自己到起点的路径更短，此时将设置 g(s)=rhs(s)，节点状态变为局部连续状态。

局部欠连续(Locally Underconsistent)：$g(s)<rhs(s)$。这种情况通常出现在父辈的某一节点突然变为障碍的情况下，造成父辈节点到起点的路径变大，从而需要修改 g(s)的值，如果节点处于这种状态，则当它由优先队列中取出时，将其 g 值设置为无穷大，即将该节点状态变为局部过连续，而局部过连续的点将会被再次添加到优先队列中，这样就可以在它下次被取出时将其作为局部过连续状态处理，最终达到局部连续状态（如果这一节点与我们要搜索的最短路径相关的话）。

LPA*维持着每个节点的到起点的估计距离: $g(s)$ 首次搜索时, $g(s)$ 的计算方式和 A*相同, 并将这个值带到下次搜索过程中.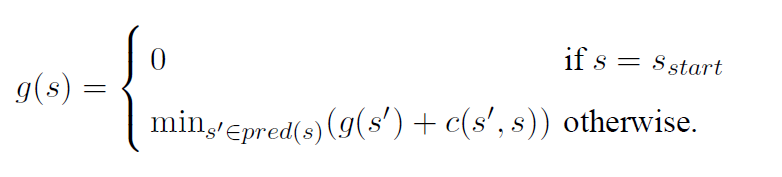
algorithm_lpa_star_g

此外 LPA*还维护着一个基于 $g(s)$ 的前瞻估计距离: $rhs(s)$.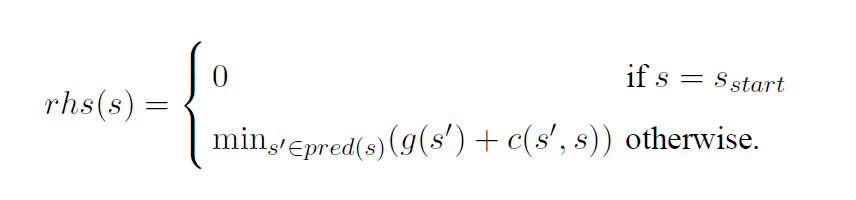
algorithm_lpa_star_rhs

A*算法维护着 OPEN 和 CLOSED 列表来避免节点被重复搜索. LPA*通过检查局部一致性来避免节点重复搜索, 不需要维护 COLSED 列表. OPEN 列表是一个优先队列, 使得 A*可以通过队列中具有最小 $f(s)$ 值的节点来进行边的扩展. LPA*也维持着一个只包含局部欠一致(locally inconsistent)节点的优先队列. 优先队列根据节点的 keys 值排列(相当于 A*的 $f(s)$ 值排列). 该 keys 是一个二维变量:

$k(s)=[k1(s),k2(s)]$

其中:

$k1(s)=min(g(s),rhs(s)+h(s))$, 相当于 A*的$f(s)$ > $k2(s)=min(g(s),rhs(s))$, 相当于 A*的$g(s)$

定义: $k(s1) \leq (s2)$ 为 $k1(s1) \leq k1(s2)$ 或者 $(k1(s1)=k1(s2) \text{ and }k2(s1) \leq k2(s2))$

伪码

算法伪码如下图所示 Algorithms LAP*
3

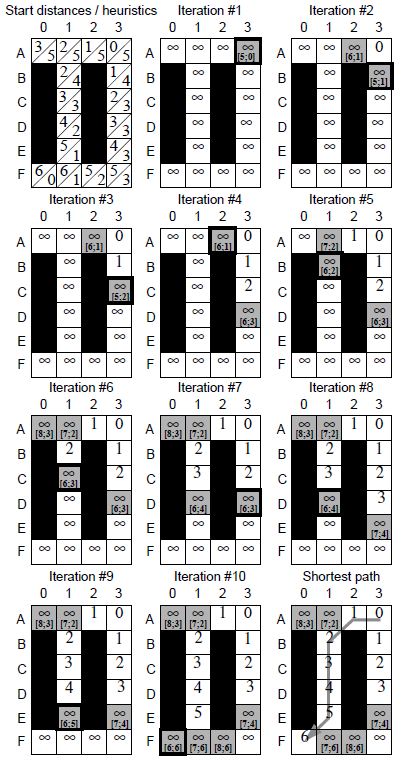
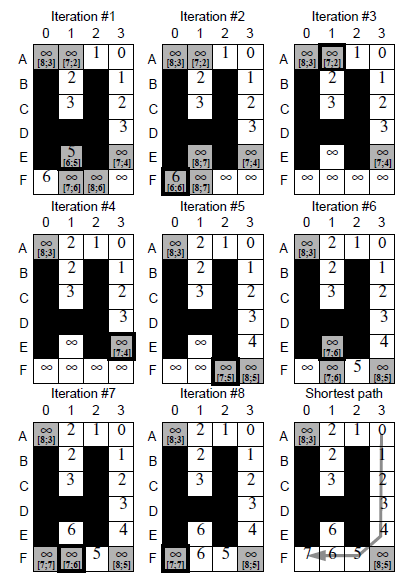
图解

第一次搜索
4

第二次搜索
5

流程

  • 初始化LPA_STAR.__init__: 初始化地图，对地图图片二值化处理，网格节点划分，若网格内包含障碍物，则该网格节点标记为障碍物: Node.is_obs = True

  • 输入需要随机产生的障碍物网格个数(可选);

  • Initialize(): 初始化所有节点的$g(s)=\infin$, $rhs(s)=\infin$, 实际实现中，不需要初始化所有节点，只需要在遇到一个新节点时初始化该节点. 起点$s_{start}$是一个局部欠一致节点, 计算$keys(s_{start})$, 并将节点$s_{start}$放入优先队列中.

  • 初始化Initialize()保证了首次调用ComputeShortestPath()是一个 A*算法。

  • 等待地图更新， 这里通过用户输入障碍物网格数来模拟地图更新。

  • 地图更新时，导致节点之间的距离DistanceCost发生变化, 调用UpdateVertex(s)更新受影响节点参数rhs和keys。这也这些节点和优先队列之间的联系也发生变化，可能成为局部一致或者局部不一致状态。

  • 重新调用ComputeShortestPath()来根据优先队列顺序展开局部不一致的节点。

    • 如果展开的节点处于局部过一致(locally overconsistent)状态, 即$g(s)>rhs(s)$, 那么将该节点设置为局部一致(locally consistent), 即$g(s)=rhs(s)$。

    • 如果展开的节点处于局部欠一致(locally underconsistent)状态，即$g(s)<rhs(s)$, 那么将该节点的g值设置为无穷大， 即$g(s)=\infin$

    • 上述两种情况中受该展开节点的g值变化会影响后置节点，所以还需要更新受其影响的节点，调用UpdateVertex(s)来更新。

  • LPA*扩展停止条件为：目标节点$s_{goal}$处于局部一致并且下一个待展开的节点keys值不小于$s_{goal}$的keys值。若搜索结束之后目标节点$s_{goal}$的g值为无穷大，那路径不存在。

  • 将目标节点$s_{goal}$的后置链表反转即可得到$s_{start}$到$s_{goal}$的路径

实现

数据结构

1
2
3
4
5
6
7
8
9
class Node(object):
    def __init__(self, pos):
        self.pos = pos          # 当前节点的位置坐标
        self.g = float('inf')   # 当前节点的g(s),g_score
        self.h = float('inf')   # 当前节点的的h(s),h_score
        self.rhs = float('inf') # rhs(s)
        self.keys = [float('inf'), float('inf')]    # 优先队列keys(s)值
        self.p = None           # 当前节点的父节点
        self.is_obs = False     # 当前节点是否是障碍物

接口

1
2
3
4
5
6
7
8
9
'''
map_path:   地图图片路径
qstart:     起点坐标 [row, col]
qgoal:      目标点坐标 [row, col]
grid_size:  网格大小（用来碰撞检测）
'''

lpa_star = LPA_STAR(map_path, qstart, qgoal, grid_size)

Planning

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101

def CalculateKey(self, s):
    '''
    the priority queue ordered by k1(f_score used in A*), then k2
    '''
    key2 = min([s.g, s.rhs])
    return [key2 + s.h, key2]

def Initialize(self):
    '''
    init
    '''
    self.U = []
    self.qstart.rhs = 0
    self.qstart.keys = [self.qstart.h, 0]
    self.U.append(self.qstart)

def UpdateVertex(self, u):
    # u = copy.deepcopy(u)
    if u.pos != self.qstart.pos:
        new_rhs = float('inf')
        # predessors = self.Predessors(u)
        predessors = self.SuccessorsCollisionFree(u)
        for pred in predessors:
            tmp_rhs = pred.g + self.DistanceCost(pred, u)
            if tmp_rhs < new_rhs:
                new_rhs = tmp_rhs
                u.p = pred
        u.rhs = new_rhs

    for node_index, node in enumerate(self.U):
        if node.pos == u.pos:
            self.U.pop(node_index)
            break

    if u.g != u.rhs:
        u.keys = self.CalculateKey(u)
        self.UInsert(u)

    return

def ComputeShortestPath(self):

    color_close = (random.randint(0, 255),
                   random.randint(0, 255),
                   random.randint(0, 255))

    while (len(self.U) != 0) and ((self.TopKey() < self.CalculateKey(self.qgoal)) or (self.qgoal.rhs != self.qgoal.g)):

        u = self.U.pop(0)
        self.DrawGrid(u.pos, color_close)

        if u.g > u.rhs:
            u.g = u.rhs
            successors = self.SuccessorsCollisionFree(u)
            for succ in successors:
                self.UpdateVertex(succ)
        else:
            u.g = float('inf')
            self.UpdateVertex(u)
            successors = self.SuccessorsCollisionFree(u)
            for succ in successors:
                self.UpdateVertex(succ)

    if self.qgoal.rhs == self.qgoal.g and self.qgoal.rhs != float('inf'):
        self.FindPath()
        print('Found Path')
        return True
    else:
        print('Not Found Path')
        return False

def Planning(self):

    num = input("input obstacle numbers: ")
    try:
        input_num = eval(num)
        if type(input_num) == int:
            self.AddObstacle(input_num)
        else:
            return
    except:
        return

    while True:
        if self.ComputeShortestPath() == False:
            return

        num = input("input obstacle numbers: ")
        try:
            input_num = eval(num)
            if type(input_num) == int:
                obstacle_set = self.AddObstacle(input_num)
                for obs in obstacle_set:
                    successors = self.SuccessorsExcludeObstacle(obs)
                    for succ in successors:
                        self.UpdateVertex(succ)
            else:
                return
        except:
            return