路径规划之 RRT_Star

RRT_Connect 相对于 RRT 虽然增加了启发式策略和贪婪思想，但他们的路径都不是最优的。搜索路径都是基于随机采样，缺少评价函数。RRT_Star 算法在 RRT 的基础上，基于代价函数来重新选择新父节点，重新布线新子节点，保证算法渐进最优解。

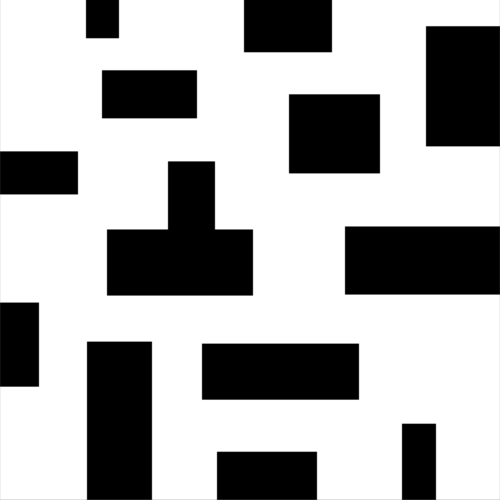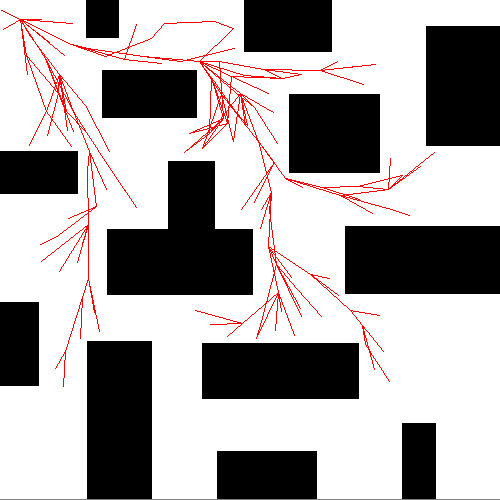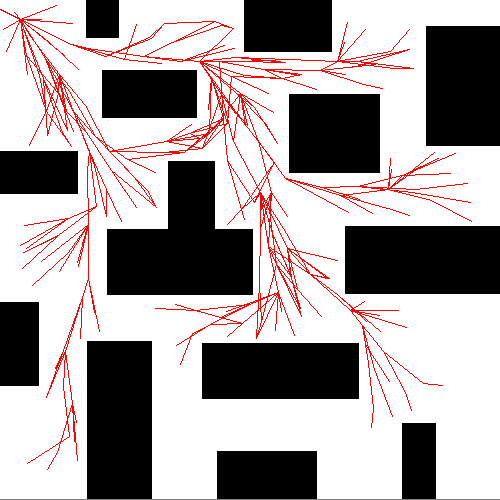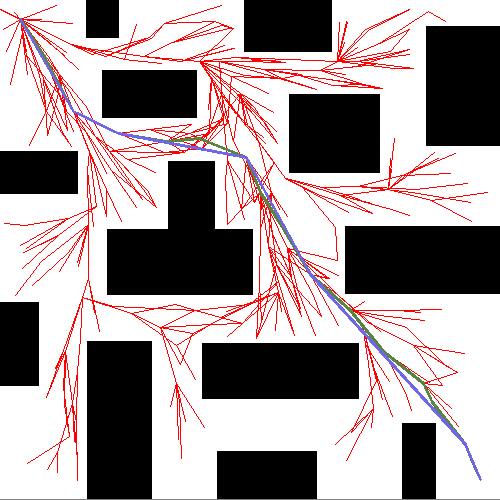
rrt_star.gif

算法描述

RRT* 构造方式和 RRT 类似，区别在于重新选择父节点和重新布线这个过程。在寻找到新节点 $q_{new}$ 时，先进行碰撞检测，若 ($q_{near}$， $q_{new}$) 没有碰撞，并不立即将新节点和新边加入到树中。而是首先重新选择父节点：寻找以 $q_{new}$ 为圆心，以半径$r$内的所有邻接节点，作为$q_{new}$ 的潜在父节点 $q_{proential_parents}$ 。然后遍历所有潜在父节点，若 $q_{protential_parents}$ 到 $q_{new}$ 无碰撞，则计算从起点 $q_{start}$ 到潜在父节点$q_{protential_parents}$，再到新节点$q_{new}$的总路径长。选择最短路径的潜在父节点(假设记为$q_{min_parent}$)作为$q_{new}$的父节点，添加边 ($q_{min_parent}, q_{new}$) 到树中。 在完成父节点的重新选择后，再对该邻域重新布线：再次遍历该邻接节点集合中除 $q_{min_parent}$ 之外的剩余节点，作为 $q_{new}$ 的潜在子节点 $q_{proential_children}$，若 $q_{new}$ 到 $q_{protential_children}$ 无碰撞，则计算从起点 $q_{start}$ 到新节点 $q_{new}$ ，再到潜在子节点 $q_{protential_children}$ 的总路径长。选择最短路径的潜在子节点 (假设记为 $q_{min_child}$ )，将该节点的父节点设置为 $q_{new}$ 的新节点，删除边 ($q_{parent_of_min_child}$, $q_{min_child}$) 添加边 ($q_{new}$, $q_{min_parent}$) 到树中。因为我们通过链表来构建树，所以设置父节点也相当于添加边；更改父节点，相当于删除了原来的边并添加新边。通过上述两次选择，使得 RRT* 达到渐进最优，并且构造树的节点和边大大减少，提高的搜索效率。

伪码

Algorithms RRT_Connect

实现

数据结构

1
2
3
4
class Node(object):
    def __init__(self, pos=[0, 0]):
        self.pos = pos
        self.parent = None

接口

1
2
3
4
5
6
7
8
9
10
11
12
13
14
'''
map_path: 地图图片路径
qstart: 起点坐标 [row, col]
qgoal: 目标点坐标 [row, col]
grid_size: 网格大小（用来碰撞检测）
step_size: 扩展步长
neighbor_radius: 邻域半径，有公式计算的，这里为简单起见，选择定制
max_steps: 最大扩展节点数
goal_prob: 增加趋向目标点概率（贪婪）
'''

rrt_star = RRT_STAR(map_path, qstart, qgoal, grid_size,
                    step_size, parent_radius, max_steps, goal_prob)

Planning

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
def Planning(self):
    '''
    RRT_STAR planning
    '''

    # 初始化树，添加起点
    vertices = []
    self.AddVertices(self.qstart, vertices)
    self.AddEdges(None, self.qstart)

    # 开始扩展
    k = 0
    while k <= self.max_steps:
        k += 1

        # 随机采样节点qrand，

        # 扩展新节点qnew
        qrand = self.GenerateRandomNode(
            [0, self.map_shape[0]], [0, self.map_shape[1]],
            self.qgoal, self.goal_prob)

        # 遍历树节点 vertices，选择距离最近的节点 qnear
        _, qnear = self.FindNearestNode(qrand, vertices)

        # 扩展新节点 qnew
        qnew = self.ExtendTree(qnear, qrand, self.step_size)

        # 判断 qnew 扩展成功，且(qnear, qnew)无碰撞
        if qnew and self.CollsionFree(qnear, qnew, self.grid_size):

            # 寻找以qnew为圆心，parent_radius为半径的圆内邻接节点neighbors_free
            neighbors_free = self.FindNeighbors(
                qnew, vertices, self.parent_radius)

            '''
            neighbors = list(filter(lambda qnode: self.Distance(
                qnode.pos, qnew.pos) < self.parent_radius, vertices))
            neighbors_free = []
            for parent in neighbors:
                if self.CollsionFree(parent, qnew, self.grid_size):
                    neighbors_free.append(parent)
            '''

            # 重新选择父节点：
            # 计算路径代价Cost(qstart, neighbors_free, qnew),
            # 选择最短路径的潜在父节点作为qnew的新父节点qnew_parent，并将新边加入到树中
            len_qnew_path, qnew_parent = self.RewireNewParent(
                qnew, vertices, neighbors_free)

            '''
            len_qnew_path = float('inf')
            qnew_parent = None
            for parent in neighbors_free:
                parent_path = self.FindPathByParentPointer(parent)
                len_parent_path = self.CalculatePathLength(parent_path)
                tmp_len_path = len_parent_path + \
                    self.Distance(qnew.pos, parent.pos)

                if tmp_len_path < len_qnew_path:
                    len_qnew_path = tmp_len_path
                    qnew_parent = parent

            self.AddVertices(qnew, vertices)
            self.AddEdges(qnew_parent, qnew)
            self.DrawEdges(self.src_map, qnew_parent, qnew)
            '''

            # 重新布线：
            # 计算neighbors_free中除qnew_parent外的路径代价Cost(qstart, qnew, neighbors_free),
            # 选择最短路径的节点qnew_children，设置其父节点为qnew，并将新边加入到树中
            if qnew_parent:
                neighbors_free.remove(qnew_parent)
            self.RewireNewChild(qnew, len_qnew_path, neighbors_free)
            '''
            qnew_children = None
            for child in neighbors_free:
                tmp_len_path = len_qnew_path + \
                    self.Distance(qnew.pos, child.pos)

                if self.CollsionFree(child, qnew, self.grid_size):
                    child_path = self.FindPathByParentPointer(child)
                    if tmp_len_path < self.CalculatePathLength(child_path):
                        qnew_children = child
                        self.AddEdges(qnew, qnew_children)
                        self.DrawEdges(self.src_map, qnew,
                                       qnew_children)
            '''

            # 检查两棵树是否相连,若相连，则完成路径规划
            if self.IsArrival(qnew, self.qgoal, self.step_size):
                print("Found")

                # 如果两棵树连上了，说明找到路径了，把最后一个节点添加到树中。
                self.AddVertices(self.qgoal, vertices)
                self.AddEdges(qnew, self.qgoal)
                self.DrawEdges(self.src_map, qnew, self.qgoal)

                # 构建路径
                path = self.FindPath(vertices)
                self.DrawPath(self.src_map, path)

                # 圆滑路径
                smooth_path = self.SmoothPath(path, self.grid_size)
                self.DrawPath(self.src_map, smooth_path)

                return True

    print("NotFound")
    return False

参考资料

[1]: Karaman S, Frazzoli E. Sampling-based algorithms for optimal motion planning[J]. The international journal of robotics research, 2011, 30(7): 846-894.
[2]: Choset. Principles of Robot Motion: Theory, Algorithms, and Implementations[J]. Proceedings of the Society for Experimental Biology & Medicine Society for Experimental Biology & Medicine, 2005, 147(1):512-512.
[3]: https://blog.csdn.net/weixin_43795921/article/details/88557317
[4]: https://www.cnblogs.com/guojun-junguo/p/10198144.html